Freelance Traveller

Running vs Standing Jumps

This article originally appeared in the November/December 2019 issue.

Once a starship is out past the 100-Diameter limit (or other declared safe jump limit), the ship can jump to the next star system. Many sources indicate (or by default give transit times appropriate for) the ship accelerating out half-way and then decelerating for the remainder leaving the ship with the same velocity as it left the planet. This ubiquitous formula for in-system transport is given by t = 2√(d/a) where t is time in seconds, d is distance (in meters or kilometers) to travel and a is acceleration in the same units per second per second (e.g. m/s² or km/s²). A 1G ship has a 9.8m/s² acceleration (though it’s not uncommon to fiat this to 10m/s² to simplify calculations). The formula for constant acceleration is t = √(2d/a); this gets to the jump point in 70% of the time, but leaves the ship with a high velocity entering jumpspace.

A jump made after constant acceleration is defined as a “Running Jump”. The default jump is a “Standing Jump”, though the only place where these jumps are defined is in GURPS Traveller which actually defines a Standing Jump as having zero velocity with respect to the destination star system. This means that it is almost certainly a Running Jump in the origin star system.

Standing Jumps take longer to position for, but are supposed to be “safer” than running jumps “In most cases, this is the safest type of jump, since it minimizes the possibility of colliding with an unanticipated particle of deep-space debris”. This article will discuss this trade-off.

We are assuming that jumping maintains the ship’s velocity, otherwise there are a lot of conservation laws that need to be adjusted – but if your preference is arriving in the destination system at the same speed as the target then one can use handwavium and say that the energy used in jumpspace adjusts for velocities. In this case a Running Jump would always be best saving time with no risk. The only outstanding question is what target is the velocity adjusted to? If one breaks out of jump due to hitting the “100D” limit of an object then that is the object the velocity is adjusted to, and is great because if the ship intersects with a random deep-space object then there cannot be a collision. What happens if the ship is programmed to come out of jump more than 100D from any object? Does it assume the velocity of the closest? The Source?

When we discuss velocity (or speed + direction) there needs to be a frame of reference that is what the object is measured moving relative to. Unfortunately there is no universal frame of reference, as Einstein demonstrated. So a Standing Jump with zero velocity relative to the planet that the ship departed from, is likely moving at 20-50 km/s relative to the Star. Using the star as a frame of reference is likely best as most object rotate around it. Stars, however, are moving on average 250 km/s rotating around the galactic super-massive black hole. Comparing them individually they average a 100 km/s velocity relative to each other. (There are some stars with significantly different relative velocities such as Kapteyn’s star at 293 km/s relative to Sol, or hyper-velocity stars such as US 708 at 1200 km/s). The ship in the destination star system would likely want to use that star as its frame of reference, so when jumping into a new Star system there is 50-150 km/s change in the velocity due to the differences in the stars’ velocities.

So when a ship precipitates out of jumpspace its velocity (relative to the destination star) will be determined by (a) the ship’s velocity relative to the planet, (b) the planet’s velocity relative to the origin star, and (c) the destination star’s velocity relative to the origin star. This needs to be compared to the velocity of the destination planet relative to the destination star. If a ship decides to perform a jump from zero speed in relation to the origin planet, there is no way to adjust the relative velocity to the destination planet. This could leave the ship travelling tens or hundreds of km/s in a direction away from the planet, so not only does it need to traverse the distance to the planet, but might need to shed velocity.

The ship could be lucky and have a velocity towards the planet, but why not plan for that? A running jump would be made in the correct direction to counter-act any undesired velocity. Let’s consider an example. Two stars travelling at 100km/s relative to each other, and two planets at opposite ends of their orbits travelling at 30km/s:

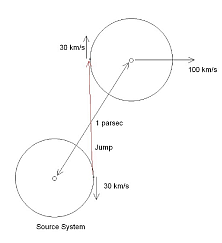Because the destination star’s velocity is to the right in the diagram, the ship will have a velocity to left relative to the destination star. As the planets are moving in opposite directions as well, the ship will be moving away from the planet at 60 km/s, for a net vector of 117 km/s away from the planet (and 104 km/s away from the star). In this example the ship will need to accelerate for 3.3 hours at 1G to come to rest relative to the planet, and then start its trip well outside of the 100D distance. For a size 8 medium iron planet the 1,287,934 km journey to the jump point would take 6.4 hours to arrive at rest relative to the planet. The ship could have taken 4.5 hours and ended up with a velocity of 159 km/s relative to the planet. If chosen in the correct direction that velocity is more than enough to negate the relative motions of all the bodies involved and give the ship a 42 km/s velocity towards the planet to get to the destination even quicker. (In a later article – jump masking, it will be shown that this option is not always available).

We have shown large savings for making the running jump. What makes the jump less safe? Travel out from the planet to the jump point and from the jump point to the destination planet will have a risk of encountering a small rock likely in some sort of orbit around the star. The escape velocity of the Sun near Earth is 42.1 km/s, so a random object will likely be less than that, so a ship making a running jump at 100-200 km/s vs a standing jump at 30 km/s relative to the star might suffer some more damage but then again at the turn-over point the ship would be travelling at 113 km/s relative to the planet. Ships have armour for just such a thing as any in-system travel is subject to micro-meteoroids.

Let’s consider encountering an object mid-jump and precipitating out. There are three places where this could happen: In the source system, in deep space, and at the destination system. At the destination system the velocity after jump is supposed to be negating as much of the relative velocity as possible, so the vector will be small, and likely in the same direction as the object giving ample time to manoeuver away from a collision. Colliding with an object in (say) the Oort cloud in the destination system or a deep-space object will effectively have a random vector in relation to the ship. The ship’s velocity vector is not the same as the trajectory to the destination system, so encountering a deep space object could have the ship moving just as likely away from the object as towards it. The ship with the Standing Jump has a velocity of zero relative to the origin planet which is billions of km away. The adding of an extra 160 km/s might be worse for the encounter or better, it is random. With two essentially random vectors the chance that they are both heading towards each other is vanishingly small, but there will still likely be some component of the vector bringing them towards each other.

Let’s look at an example: a 100-ton scout ship encounters an object in deep space. It needs to out-mass the ship, which would mass 1,500,000 kg or so. This means that the 100D limit for such an object is 170m (using the rules from last issue), or 675m using the old rules. If the ship is travelling at only 30km/s towards the object then there is about 6ms to react. If it is travelling at 190 km/s then 1ms. Not something that a human could react to. There is only about a 2% chance that both vectors are in the same 45° cone pointing towards each other, so at least 75% of the speed is in a tangential direction. The object will likely move about 120m in the time it takes for the ship to close, even at half that movement a scout ship is only 24m wide and a collision will likely not occur.

So there is no significant safety concern adding a larger random vector to another random vector to avoid intersecting a different random vector where the object is 1/100th the size of the encounter area. It can still happen, but not predictably.
The last consideration is another ship at the 100D jump point making a jump. If the ship is travelling to or from a different system then the optimal jump location will be completely different. If the ship is going to the same system, then it would have been observed making the jump just ahead of the ship, but even then it would have moved away – time in jump is not a constant. Lastly is a ship on a reciprocal course, e.g. it is about to leave the destination system for the system where the players ship is. As the vectors are the inverse, the ship will be (with the exception of one component) also opposite so almost zero chance of collision.

Conclusion: No commercial ship is going to take extra time to travel on the very slim risk involved in a Running Jump. So take 30% off the given travel times to jump points. Military ships flying in formation are a likely exception.